
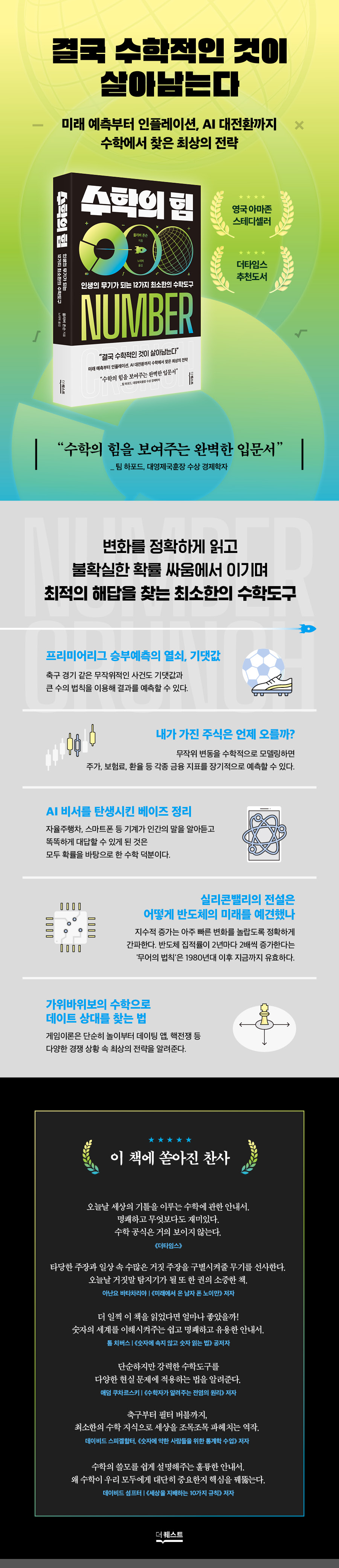
The power of mathematics
 |
Description
Book Introduction
“In the end, the mathematical survives.” In a rapidly changing world, mathematics is always the right tool. Can I predict whether my stocks will rise or fall? What are the odds that Tottenham will score in today's Premier League game? What's the "infallible" strategy for crucial decision-making situations? There's a powerful tool that can instantly answer all these questions. It's mathematics. Whether you're a math nerd or not, math solves almost every problem you face in life. Very easy and simple, but accurate. The mathematics covered in "The Power of Mathematics" is not a fancy specialized knowledge that you can show off to others or need to solve problems. This is a book about the power that will 'really' change your life. |
- You can preview some of the book's contents.
Preview
index
Introduction: If we look at the world through the language of mathematics
Part 1.
Read the Changes Beyond the Numbers: Structure
Chapter 1.
A good picture is worth a thousand words.
See changes at a glance with graphs
Constant change vs. moving change
The Pitfalls of Overly Accurate Graphs
Chapter 2.
How to find your way through the number jungle
Number anxiety that comes from watching the news
If you cultivate a sense of smell, you can see the government budget plan.
Think about it in pieces
How to avoid being fooled by seemingly good numbers
The Mathematical Reason My Inbox Is Messy
Chapter 3.
Why Our Pandemic Predictions Were Wrong
The change didn't come suddenly.
The Key to Reading Very, Very Rapid Changes: Logarithmic Scale
Why Your Prediction Failed
The Secret of Rising Stock Charts
How Silicon Valley Legends Read the Future
Chapter 4.
The equation that captures the changes in the world
Can you predict the weather?
The more you segment the movement, the more you see the axis of change.
The flapping of a butterfly's wings makes predictions difficult.
A single formula that pierces through the age of uncertainty
Part 2.
How to Win at the Odds:
randomness
Chapter 5.
God does not play dice
Even things that happen by chance have rules.
What happens when you flip a coin 10,000 times
Liverpool's odds of losing today's match: Expected Goals
Where Irregular Data Gathers: The Central Limit Theorem
There are always exceptions
Chapter 6.
How to avoid being fooled by attractive false answers
How reliable is that judgment?
The minimum standard for judging right and wrong
Gaining weight doesn't mean you're overeating.
The numerical calculations are accurate, but the graphs are rough.
A straight line that uncovers hidden threats
Chapter 7.
How to use probability
Dependency of events
Probability of B given A
Reconstructing the probability into a table
If you miss the asymmetry of risk,
infectious diseases with many outbreaks
Uncovering Hidden Inequalities
Chapter 8.
Turning the odds around reveals a winning strategy.
The mathematician who went to the casino
Bayes' theorem changed the course of war
Creating personalized medical tests with Bayes factors
Who will dominate the market?
Part 3.
Shining brighter in complex modern society
The Power of Math: Information
Chapter 9.
In a world where everything becomes data
The story begins with Claude Shannon.
How mathematicians deal with randomness
Signal and noise
Get the data you need, not just a lot of data.
Maximum effect at minimum cost
Mathematical Wisdom for Dealing with Bias
The data tells us the best bet
Chapter 10.
Predicting the predictable future
Good news: Stock price prediction models are possible.
The Math Behind Google's Search Engine
The near future comes gradually
A mathematical understanding of word of mouth
Demand can be predicted
Chapter 11.
Understanding the nature of numbers reveals the world.
The illusion of 'accurate and unchanging' measurements
Patterns are less common than you think, and miracles are more common than you think.
Assessing disease response capabilities by government
Who is the best boy group of all time?
Conditions for a suitable picture
Chapter 12.
Mathematics: Finding the Best Strategy at the Moment of Choice
Even rock-paper-scissors has its best strategy.
The Prisoner's Dilemma: Cooperating with an Opponent You Don't Like
Zero-sum games: Sometimes no strategy is strategy.
Minimax Strategy: Big profits, small losses
When desire and reason clash, mathematics provides the answer.
When game theory meets AI
Part 4.
In the end, the mathematical survives.
Chapter 13.
Lessons learned from mistakes
1.
Look at the family
2.
The world is a confusing place
3.
Don't focus too much on the past
4.
You can't just pick and choose data to your liking.
5.
The model has limitations
6.
Beware of the trap of groupthink
7.
Not everything goes as planned.
8.
Admit your mistakes
9.
Have a balanced perspective
10.
Mathematics is the right tool
Glossary of Terms
Further Reading
Part 1.
Read the Changes Beyond the Numbers: Structure
Chapter 1.
A good picture is worth a thousand words.
See changes at a glance with graphs
Constant change vs. moving change
The Pitfalls of Overly Accurate Graphs
Chapter 2.
How to find your way through the number jungle
Number anxiety that comes from watching the news
If you cultivate a sense of smell, you can see the government budget plan.
Think about it in pieces
How to avoid being fooled by seemingly good numbers
The Mathematical Reason My Inbox Is Messy
Chapter 3.
Why Our Pandemic Predictions Were Wrong
The change didn't come suddenly.
The Key to Reading Very, Very Rapid Changes: Logarithmic Scale
Why Your Prediction Failed
The Secret of Rising Stock Charts
How Silicon Valley Legends Read the Future
Chapter 4.
The equation that captures the changes in the world
Can you predict the weather?
The more you segment the movement, the more you see the axis of change.
The flapping of a butterfly's wings makes predictions difficult.
A single formula that pierces through the age of uncertainty
Part 2.
How to Win at the Odds:
randomness
Chapter 5.
God does not play dice
Even things that happen by chance have rules.
What happens when you flip a coin 10,000 times
Liverpool's odds of losing today's match: Expected Goals
Where Irregular Data Gathers: The Central Limit Theorem
There are always exceptions
Chapter 6.
How to avoid being fooled by attractive false answers
How reliable is that judgment?
The minimum standard for judging right and wrong
Gaining weight doesn't mean you're overeating.
The numerical calculations are accurate, but the graphs are rough.
A straight line that uncovers hidden threats
Chapter 7.
How to use probability
Dependency of events
Probability of B given A
Reconstructing the probability into a table
If you miss the asymmetry of risk,
infectious diseases with many outbreaks
Uncovering Hidden Inequalities
Chapter 8.
Turning the odds around reveals a winning strategy.
The mathematician who went to the casino
Bayes' theorem changed the course of war
Creating personalized medical tests with Bayes factors
Who will dominate the market?
Part 3.
Shining brighter in complex modern society
The Power of Math: Information
Chapter 9.
In a world where everything becomes data
The story begins with Claude Shannon.
How mathematicians deal with randomness
Signal and noise
Get the data you need, not just a lot of data.
Maximum effect at minimum cost
Mathematical Wisdom for Dealing with Bias
The data tells us the best bet
Chapter 10.
Predicting the predictable future
Good news: Stock price prediction models are possible.
The Math Behind Google's Search Engine
The near future comes gradually
A mathematical understanding of word of mouth
Demand can be predicted
Chapter 11.
Understanding the nature of numbers reveals the world.
The illusion of 'accurate and unchanging' measurements
Patterns are less common than you think, and miracles are more common than you think.
Assessing disease response capabilities by government
Who is the best boy group of all time?
Conditions for a suitable picture
Chapter 12.
Mathematics: Finding the Best Strategy at the Moment of Choice
Even rock-paper-scissors has its best strategy.
The Prisoner's Dilemma: Cooperating with an Opponent You Don't Like
Zero-sum games: Sometimes no strategy is strategy.
Minimax Strategy: Big profits, small losses
When desire and reason clash, mathematics provides the answer.
When game theory meets AI
Part 4.
In the end, the mathematical survives.
Chapter 13.
Lessons learned from mistakes
1.
Look at the family
2.
The world is a confusing place
3.
Don't focus too much on the past
4.
You can't just pick and choose data to your liking.
5.
The model has limitations
6.
Beware of the trap of groupthink
7.
Not everything goes as planned.
8.
Admit your mistakes
9.
Have a balanced perspective
10.
Mathematics is the right tool
Glossary of Terms
Further Reading
Detailed image
Into the book
Once you understand these concepts, you'll see more ways to use them to understand the world.
It's nearly impossible to predict what news stories will make headlines in the next decade, but with these mathematical tools, you'll be in a better position to rationally interpret whatever news you see and separate signal from noise.
By learning to think mathematically through this book and viewing the latest information through a mathematical lens, you will be ready to understand the world for yourself.
--- From "Introduction: Seeing the World Through the Language of Mathematics"
Elon Musk acquired Twitter for $44 billion.
In January 2022, Apple became the first company to be valued at over $3 trillion.
When you come across numbers like these, you tend to get confused.
But as responsible citizens, we must try to understand what these numbers mean.
In this chapter, we'll look at some tips for dealing with these numbers and getting a general sense of them.
This valuable skill can be applied to countless real-world situations where we are bombarded with statistics every day.
--- From "A picture is worth a thousand words"
This exponential function can be used to very well predict the future of a phenomenon.
As we will see, exponential functions appear in explaining biological problems such as bacteria and population growth, financial and economic problems such as money growing over time, and the performance improvements of next-generation computers.
Exponential functions can help us understand all of these phenomena much better, and by properly representing them on a graph, we can more easily estimate the pattern of increase in various numbers.
--- From Chapter 3, “Why Were Our Pandemic Predictions Wrong?”
Adding up all the fractional scoring results from analyzing the shots attempted by a team gives the total expected goals scored in a game.
(Omitted) The idea of dividing a game into its individual components and measuring those elements is also the core of baseball's Moneyball philosophy, which pursues low cost and high efficiency.
Methods for calculating expected scores are also applied to financial engineering, which utilizes mathematical models to create derivatives based on stocks that reflect the volatility of the market itself.
People who make money in the financial markets are interested in these methods.
--- From "Chapter 5 God Does Not Play Dice"
A branch of statistics called Bayesian inference is based on Bayes' theorem.
This concept underpins the technology that allows Siri to recognize voices, smartphones to automatically categorize photos by subject, and modern machine learning algorithms (or, more positively, AI) that will one day control self-driving cars.
To look at it from the perspective of data and hypothesis, let's say event A is 'the microphone picked up some sound' and event B is 'the person is saying the word fish'.
Given a large amount of training data, a set of people saying fish, we can figure out the probability that the microphone will correctly understand that word when it receives it.
Next, we can use Bayes' theorem to calculate the probability that a person said "fish" when a sound was received from the microphone.
--- From "Chapter 7 How to Use Probability"
Hamming's research was ahead of its time in the modern era of big data.
In the era of big data, vast amounts of data on all phenomena can be easily measured with cheap sensors, reported via fast, ubiquitous wireless networks, and stored and processed by high-performance computers, but his conclusions still hold true today.
In other words, just because we can measure something doesn't mean we should measure it.
It is more important to use the right indicator at the right time than to consider all indicators at the same time.
--- From "Chapter 11: Understanding the Essence of Numbers Reveals the World"
The final message is that mathematics is likely the right tool to use to understand the situation.
How functions grow, what role randomness and uncertainty play, and what information theory tells us about information correlated with filter bubbles.
Whatever the question, mathematical techniques provide insight in a way that is free from emotions and personal biases.
(syncopation)
Just knowing that the very act of asking questions like, "Are these numbers reasonable?" or "What is the margin of error for those numbers?" is important will enable anyone to think more intelligently when using mathematical principles to deal with information about the world.
It's nearly impossible to predict what news stories will make headlines in the next decade, but with these mathematical tools, you'll be in a better position to rationally interpret whatever news you see and separate signal from noise.
By learning to think mathematically through this book and viewing the latest information through a mathematical lens, you will be ready to understand the world for yourself.
--- From "Introduction: Seeing the World Through the Language of Mathematics"
Elon Musk acquired Twitter for $44 billion.
In January 2022, Apple became the first company to be valued at over $3 trillion.
When you come across numbers like these, you tend to get confused.
But as responsible citizens, we must try to understand what these numbers mean.
In this chapter, we'll look at some tips for dealing with these numbers and getting a general sense of them.
This valuable skill can be applied to countless real-world situations where we are bombarded with statistics every day.
--- From "A picture is worth a thousand words"
This exponential function can be used to very well predict the future of a phenomenon.
As we will see, exponential functions appear in explaining biological problems such as bacteria and population growth, financial and economic problems such as money growing over time, and the performance improvements of next-generation computers.
Exponential functions can help us understand all of these phenomena much better, and by properly representing them on a graph, we can more easily estimate the pattern of increase in various numbers.
--- From Chapter 3, “Why Were Our Pandemic Predictions Wrong?”
Adding up all the fractional scoring results from analyzing the shots attempted by a team gives the total expected goals scored in a game.
(Omitted) The idea of dividing a game into its individual components and measuring those elements is also the core of baseball's Moneyball philosophy, which pursues low cost and high efficiency.
Methods for calculating expected scores are also applied to financial engineering, which utilizes mathematical models to create derivatives based on stocks that reflect the volatility of the market itself.
People who make money in the financial markets are interested in these methods.
--- From "Chapter 5 God Does Not Play Dice"
A branch of statistics called Bayesian inference is based on Bayes' theorem.
This concept underpins the technology that allows Siri to recognize voices, smartphones to automatically categorize photos by subject, and modern machine learning algorithms (or, more positively, AI) that will one day control self-driving cars.
To look at it from the perspective of data and hypothesis, let's say event A is 'the microphone picked up some sound' and event B is 'the person is saying the word fish'.
Given a large amount of training data, a set of people saying fish, we can figure out the probability that the microphone will correctly understand that word when it receives it.
Next, we can use Bayes' theorem to calculate the probability that a person said "fish" when a sound was received from the microphone.
--- From "Chapter 7 How to Use Probability"
Hamming's research was ahead of its time in the modern era of big data.
In the era of big data, vast amounts of data on all phenomena can be easily measured with cheap sensors, reported via fast, ubiquitous wireless networks, and stored and processed by high-performance computers, but his conclusions still hold true today.
In other words, just because we can measure something doesn't mean we should measure it.
It is more important to use the right indicator at the right time than to consider all indicators at the same time.
--- From "Chapter 11: Understanding the Essence of Numbers Reveals the World"
The final message is that mathematics is likely the right tool to use to understand the situation.
How functions grow, what role randomness and uncertainty play, and what information theory tells us about information correlated with filter bubbles.
Whatever the question, mathematical techniques provide insight in a way that is free from emotions and personal biases.
(syncopation)
Just knowing that the very act of asking questions like, "Are these numbers reasonable?" or "What is the margin of error for those numbers?" is important will enable anyone to think more intelligently when using mathematical principles to deal with information about the world.
--- From "Chapter 13 Lessons Learned from Errors"
Publisher's Review
★★★★★
“A perfect introduction to the power of mathematics.”
Tim Harford, MBE-winning economist
Professor Oliver Johnson, who has become a hot topic on Twitter with 43,000 followers for his easy-to-understand explanations of pandemic-related statistics, doesn't follow the textbook's exact order; instead, he introduces 12 tools for effectively applying math in everyday life.
You can read complex bills and stock charts using a few familiar math concepts, such as graphs, exponential logarithms, etc.
The law of large numbers and Bayes' theorem, which govern probability, teach you how to protect your capital in a bet with a friend.
Without mathematics, we wouldn't be able to make calls on our smartphones anywhere, Siri would understand what we're saying, and NASA would be able to send spacecraft to the moon.
There are very few formulas in this book.
With simple pictures and charts, we'll show you how math moves the world and how it can improve your life.
If you can understand mathematics and think like a mathematician, you are in a better position to understand the world.
The most powerful weapon to understand change and innovation
How does math solve more problems with less worry?
In a world where calculators crunch lengthy formulas and AI answers questions with ease, why learn math? The answers lie within the questions.
Because solving complex problems easily is the essence of mathematics.
A single, seemingly insincere graph can explain all sorts of phenomena, from interest and insurance premiums to soccer player transfer fees and bacterial growth.
What if a simple mathematical rule called "doubling" could provide a prediction that remained unchanged for over 50 years? In 1965, Silicon Valley legend and innovator Gordon Moore foresaw the evolution of the semiconductor industry based on his insights into the law of exponential growth, a prediction that remains valid to this day.
Need to tackle a challenging problem or handle very large numbers? Math can help.
Start with the easy things, not the hard things.
In Chapter 2, you will learn how to read numbers “roughly but accurately.”
Knowing the principles of approximation and what to watch out for, when you see a claim on social media saying, "Let's cut congressmen's salaries in half to raise unemployment benefits," you can easily calculate how much unemployment benefits per person would increase.
Even natural phenomena that seem unpredictable at first glance, such as weather or epidemics, reveal patterns when broken down into very small pieces.
In Chapter 4, we will examine the core concepts of differentiation using only pictures, without complex formulas, and understand how the movement of a pendulum or the number of hospital admissions changes.
Mathematics easily explains every change you encounter.
★★★★★
“Professor Johnson uses simple but powerful mathematical tools to
“It provides useful and timely insights.”
Adam Kucharsky, author of "A Mathematician Explains How Contagion Works"
“An excellent guide that explains the usefulness of mathematics in an easy-to-understand way.”
David Sumpter, author of 10 Rules for Rule the World
In an age of uncertainty, technology leaves only correct predictions and successful strategies.
No one wants to fail.
Whether you're reading predictions before a soccer match or getting your fortune told on New Year's Eve, everyone strives to accurately predict what will happen in the future.
But we often struggle with mistakes, misjudgments, and the overwhelming amount of information.
How can I minimize the chance of being wrong and retain only the strategies I need? Let's say I've discovered a promising startup.
How fast and how long can this company grow? Or, if I were betting with a friend on whether a soccer game would be won today, how much would I need to stake on my prediction to break even? A thorough understanding of probability, combined with a few mathematical tools, can easily answer these questions.
This book reveals the secret through several rules of probability, such as the law of large numbers and Bayes' theorem.
Even in a jungle of random changes and data, mathematics provides the most effective strategies.
If you absolutely want to win at rock-paper-scissors, the answer is to not think too much and just play anything.
Even exchange rate graphs that seem completely unpredictable move in a specific direction over the long term.
It's all thanks to math that Netflix recommends content you're most likely to be interested in, and that Google searches only return relevant results.
Very simple mathematical rules govern the world.
Thinking mathematically is no different from finding what I need most quickly, increasing my chances of success by preparing for risks, and looking into the future.
Because even at this very moment, all changes ultimately start from mathematics.
* Praise for this book
“It gives you a weapon to distinguish between valid claims and countless false claims.”
Ananyo Bhattacharya, author of "The Man from the Future"
“From soccer to filter bubbles,
“A masterpiece that delves into the world with minimal mathematical knowledge.”
David Spiegelhalter, author of Statistics for Numbers
“How I wish I had read this book sooner!
“A simple, clear, and useful guide to understanding the world of numbers.”
Tom Chivers, author of "How to Read Numbers Without Being Fooled by Them"
“Clear and, above all, fun.”
_The Times
“A perfect introduction to the power of mathematics.”
Tim Harford, MBE-winning economist
Professor Oliver Johnson, who has become a hot topic on Twitter with 43,000 followers for his easy-to-understand explanations of pandemic-related statistics, doesn't follow the textbook's exact order; instead, he introduces 12 tools for effectively applying math in everyday life.
You can read complex bills and stock charts using a few familiar math concepts, such as graphs, exponential logarithms, etc.
The law of large numbers and Bayes' theorem, which govern probability, teach you how to protect your capital in a bet with a friend.
Without mathematics, we wouldn't be able to make calls on our smartphones anywhere, Siri would understand what we're saying, and NASA would be able to send spacecraft to the moon.
There are very few formulas in this book.
With simple pictures and charts, we'll show you how math moves the world and how it can improve your life.
If you can understand mathematics and think like a mathematician, you are in a better position to understand the world.
The most powerful weapon to understand change and innovation
How does math solve more problems with less worry?
In a world where calculators crunch lengthy formulas and AI answers questions with ease, why learn math? The answers lie within the questions.
Because solving complex problems easily is the essence of mathematics.
A single, seemingly insincere graph can explain all sorts of phenomena, from interest and insurance premiums to soccer player transfer fees and bacterial growth.
What if a simple mathematical rule called "doubling" could provide a prediction that remained unchanged for over 50 years? In 1965, Silicon Valley legend and innovator Gordon Moore foresaw the evolution of the semiconductor industry based on his insights into the law of exponential growth, a prediction that remains valid to this day.
Need to tackle a challenging problem or handle very large numbers? Math can help.
Start with the easy things, not the hard things.
In Chapter 2, you will learn how to read numbers “roughly but accurately.”
Knowing the principles of approximation and what to watch out for, when you see a claim on social media saying, "Let's cut congressmen's salaries in half to raise unemployment benefits," you can easily calculate how much unemployment benefits per person would increase.
Even natural phenomena that seem unpredictable at first glance, such as weather or epidemics, reveal patterns when broken down into very small pieces.
In Chapter 4, we will examine the core concepts of differentiation using only pictures, without complex formulas, and understand how the movement of a pendulum or the number of hospital admissions changes.
Mathematics easily explains every change you encounter.
★★★★★
“Professor Johnson uses simple but powerful mathematical tools to
“It provides useful and timely insights.”
Adam Kucharsky, author of "A Mathematician Explains How Contagion Works"
“An excellent guide that explains the usefulness of mathematics in an easy-to-understand way.”
David Sumpter, author of 10 Rules for Rule the World
In an age of uncertainty, technology leaves only correct predictions and successful strategies.
No one wants to fail.
Whether you're reading predictions before a soccer match or getting your fortune told on New Year's Eve, everyone strives to accurately predict what will happen in the future.
But we often struggle with mistakes, misjudgments, and the overwhelming amount of information.
How can I minimize the chance of being wrong and retain only the strategies I need? Let's say I've discovered a promising startup.
How fast and how long can this company grow? Or, if I were betting with a friend on whether a soccer game would be won today, how much would I need to stake on my prediction to break even? A thorough understanding of probability, combined with a few mathematical tools, can easily answer these questions.
This book reveals the secret through several rules of probability, such as the law of large numbers and Bayes' theorem.
Even in a jungle of random changes and data, mathematics provides the most effective strategies.
If you absolutely want to win at rock-paper-scissors, the answer is to not think too much and just play anything.
Even exchange rate graphs that seem completely unpredictable move in a specific direction over the long term.
It's all thanks to math that Netflix recommends content you're most likely to be interested in, and that Google searches only return relevant results.
Very simple mathematical rules govern the world.
Thinking mathematically is no different from finding what I need most quickly, increasing my chances of success by preparing for risks, and looking into the future.
Because even at this very moment, all changes ultimately start from mathematics.
* Praise for this book
“It gives you a weapon to distinguish between valid claims and countless false claims.”
Ananyo Bhattacharya, author of "The Man from the Future"
“From soccer to filter bubbles,
“A masterpiece that delves into the world with minimal mathematical knowledge.”
David Spiegelhalter, author of Statistics for Numbers
“How I wish I had read this book sooner!
“A simple, clear, and useful guide to understanding the world of numbers.”
Tom Chivers, author of "How to Read Numbers Without Being Fooled by Them"
“Clear and, above all, fun.”
_The Times
GOODS SPECIFICS
- Date of issue: February 21, 2024
- Page count, weight, size: 336 pages | 476g | 148*215*20mm
- ISBN13: 9791140708437
- ISBN10: 1140708430
You may also like
카테고리
korean


korean


![ELLE 엘르 스페셜 에디션 A형 : 12월 [2025]](http://librairie.coreenne.fr/cdn/shop/files/b8e27a3de6c9538896439686c6b0e8fb.jpg?v=1766436872&width=3840)























