Partie 1
La veille de la naissance des fonctions trigonométriques

Arpentage et géométrie / Similitude des triangles / Similitude des pyramides / Similitude et dimensions de la Terre

Partie 2
Notions fondamentales de trigonométrie

Naissance des fonctions trigonométriques / Sinus / Variations des valeurs du sinus / Cosinus / Variations des valeurs du cosinus / Tangente / Variations des valeurs de la tangente /

Vous voulez en savoir plus ? Chronique
- Le nombre nécessaire pour remplir toute la « ligne verticale » - Qu'est-ce qu'un nombre irrationnel ?
- Variable « x » qui change en fonction des conditions, constante « a » déterminée par une seule valeur
- Renvoie un nombre pour chaque nombre.
La relation correspondante est une « fonction ».

Partie 3
Formules importantes des fonctions trigonométriques

Relation entre le sinus et le cosinus / sinus, cosinus et tangente / Théorème de Pythagore / Théorème du cosinus / Théorème du sinus / Théorème d'addition 1 et 2 / Fonctions trigonométriques et l'Almageste / Ptolémée / Exercices de trigonométrie

Vous voulez en savoir plus ? Chronique
- Qui était Pythagore, le découvreur du théorème du cube ?
- Démontrons le « théorème de Ptolémée » à l'aide du théorème du cosinus.
- Où les fonctions trigonométriques peuvent-elles être utiles ? - Dans le domaine de la mécanique quantique

Partie 4
Du « triangle » à la « vague »

Fonctions trigonométriques et cercle trigonométrique / Fonctions trigonométriques des angles / Degrés radiaux / Courbes sinusoïdales / Courbes cosinusoïdales / Courbes tangentes / Éléments de base des ondes / Amplitude et période / Superposition d'ondes / Ondes sismiques / Ondes sonores / Ondes électromagnétiques 1 et 2 / Ondes électroniques 1 et 2

Vous voulez en savoir plus ? Chronique
- Les « coordonnées » relient les formules et les formes
- Où les fonctions trigonométriques peuvent-elles être utiles ? - Dans le domaine de la synthèse vocale

Partie 5
Fonctions trigonométriques et transformées de Fourier

Le monde entouré d'ondes / Dérivation du sinus ①~③ / Dérivation du cosinus / Intégration des fonctions trigonométriques ①~② / Orthogonalité des fonctions trigonométriques / Transformée de Fourier / Applications de la transformée de Fourier / Joseph Fourier

Vous voulez en savoir plus ? Rubrique
- L'«orthogonalité» d'une fonction peut être comprise comme l'«orthogonalité» d'un vecteur.
Où les fonctions trigonométriques peuvent-elles être utiles ? – Analyse sismique en pratique

Partie 6
Développement des fonctions trigonométriques

Cours de trigonométrie / Leonhard Euler

- Section Données
Définitions des fonctions trigonométriques / Formules des fonctions trigonométriques / Tableau des rapports trigonométriques

4.
Rédaction, révision et collaboration
Koichi Kajiwara / Docteur en ingénierie, responsable du département de recherche expérimentale sur la prévention des catastrophes, Institut national japonais des sciences et technologies de la prévention des catastrophes
Hitoshi Mizutani / Rédacteur en chef de Newton Japan, ancien professeur de recherche planétaire à l'Institut des sciences spatiales
Junichi Yamagishi / Professeur associé, Division de recherche en sciences du contenu, Institut national d'informatique, Japon ; Docteur en ingénierie
Wada Sumio 和田純夫 / Maître de conférences à temps plein, École supérieure d'études culturelles interdisciplinaires, Université de Tokyo, Japon.
Docteur en sciences
Kenji Ueno / Docteur ès sciences, directeur de l'Institut de recherche en mathématiques Sekikowa, Université de Yokkaichi, Japon
Masaaki Hiramatsu / Professeur adjoint, Observatoire astronomique national du Japon, Observatoire du Chili, Docteur ès sciences

1.
Importance de la publication

Comprenez les principes des fonctions trigonométriques grâce aux images !

Que sont les fonctions trigonométriques ? En termes simples, les fonctions trigonométriques sont des outils qui expliquent clairement la relation entre les mesures des angles et les longueurs des côtés d’un triangle.
Une utilisation très basique consiste à déterminer avec précision des objets difficiles à mesurer directement, comme la hauteur d'une montagne.
Cependant, les fonctions trigonométriques ne sont pas uniquement utilisées pour les triangles.
Les fonctions trigonométriques étant étroitement liées aux ondes, elles sont également utiles pour examiner les propriétés des ondes.
Par conséquent, les fonctions trigonométriques sont absolument nécessaires en physique et en ingénierie, qui traitent des « ondes » telles que les ondes électromagnétiques et les ondes sonores (voix).
Cependant, lorsque les gens entendent les termes « fonctions trigonométriques » ou « sinus, cosinus, tangente », beaucoup pensent que « les mathématiques sont difficiles à comprendre même si on mémorise toutes les formules et tous les théorèmes compliqués ».
En fait, il existe différentes formules pour les fonctions trigonométriques.
Cependant, si vous vous contentez de mémoriser la formule sans comprendre le contexte et les fondements de sa création, il vous sera difficile de l'utiliser pleinement.
Autrement dit, si vous connaissez clairement le contexte et les fondements d'une formule, cela vous aidera grandement à vous en souvenir et à l'utiliser.

Ce livre, « Le monde des fonctions trigonométriques », explique clairement, à l'aide d'illustrations en couleur, comment les fonctions trigonométriques sont nées et se sont développées, quels sont leurs principes de base et leurs principaux contenus, et comment elles sont actuellement utilisées.
En outre, la relation entre les fonctions trigonométriques et les ondes telles que les ondes électromagnétiques, les ondes sonores et les ondes sismiques, ainsi que des domaines avancés tels que les fonctions trigonométriques et le calcul, l'orthogonalité des fonctions trigonométriques et les transformées de Fourier sont présentés de manière facile à comprendre à l'aide d'aides visuelles.
Le verso du livre contient un recueil séparé de définitions des fonctions trigonométriques, un recueil de formules importantes et un tableau des rapports trigonométriques, vous permettant ainsi de vérifier immédiatement et à tout moment les informations essentielles.
À première vue, les fonctions trigonométriques peuvent sembler être une liste d'équations difficiles, mais je crois qu'en examinant leur fonctionnement étape par étape, vous serez certainement capable d'en saisir le sens et de les utiliser librement.

2.
Fonction spéciale

Des illustrations de première qualité qui vous aident à comprendre les principes de la trigonométrie visuellement.
Il existe de nombreuses formules pour les fonctions trigonométriques.
Mais plus important encore que la formule elle-même, c'est de comprendre les principes qui permettent de l'établir.
En effet, il est impossible de gérer correctement diverses situations d'application si l'on se contente de mémoriser le contenu sans en comprendre les principes.
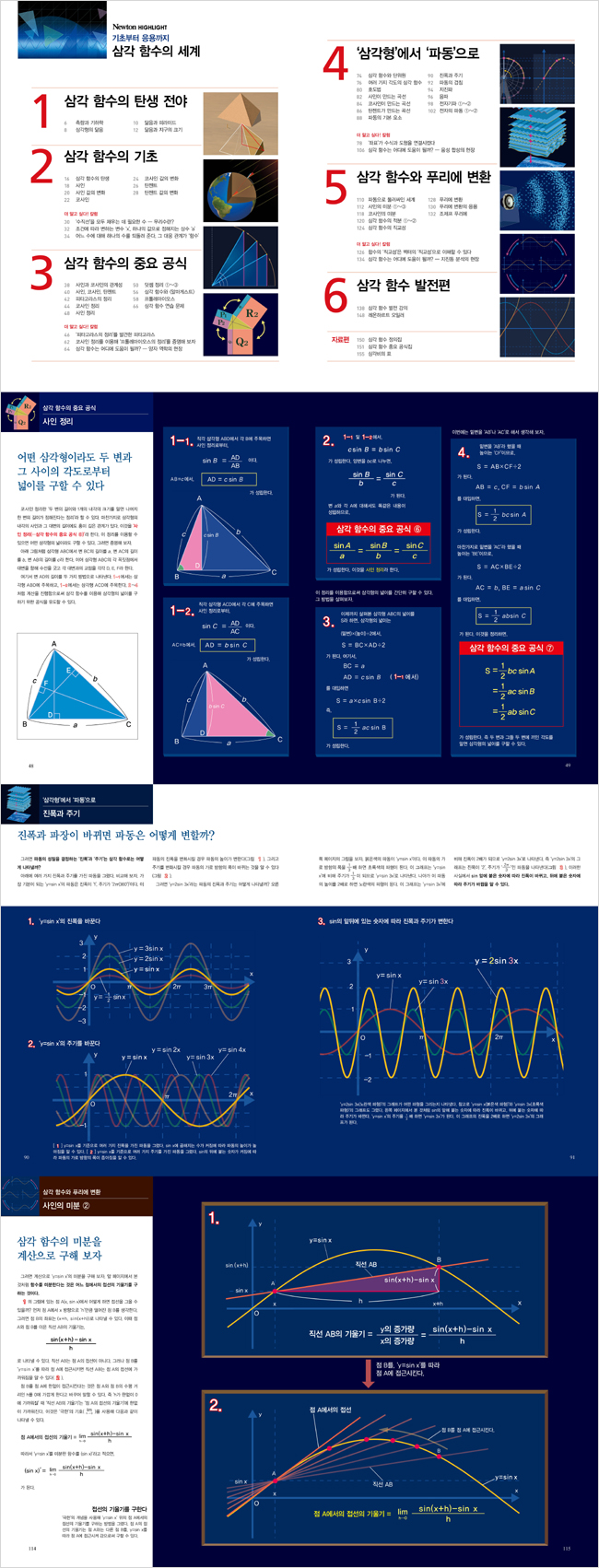
Ce livre, « Le monde des fonctions trigonométriques », est structuré de manière à ce que chacun puisse facilement comprendre les principes fondamentaux grâce à des illustrations précises qui confirment visuellement les principes mathématiques.

Un résumé complet des origines, des concepts de base, des formules importantes et des exemples d'application des fonctions trigonométriques.
On dit que la trigonométrie a débuté avec l'arpentage et les observations astronomiques dans la Grèce et l'Égypte antiques, et s'est développée en Inde et en Arabie.
Nous apprendrons pourquoi les cordes, les arcs, les angles au centre et les angles centraux sont importants dans les fonctions trigonométriques à travers le processus de création des fonctions trigonométriques.
De plus, la relation entre le sinus, le cosinus et la tangente est expliquée à travers la compréhension des concepts de base.
À partir de ces concepts de base, vous développerez la capacité de dériver des formules importantes, puis d'utiliser ces formules pour en dériver d'autres, ce qui vous permettra de faire face à diverses situations d'application.


Introduction à diverses ressources pédagogiques, notamment les fonctions trigonométriques, la synthèse vocale et l'analyse des séismes.
Les fonctions trigonométriques ne s'appliquent pas simplement aux triangles.
Les fonctions trigonométriques sont fondamentalement liées aux ondes.
En comparant les courbes créées par les sinus, les cosinus et les tangentes, et les caractéristiques des ondes telles que les ondes électromagnétiques (lumière visible, ondes radio et infrarouges), ainsi que les ondes sonores et sismiques, nous expliquons en détail comment elles sont utilisées, dans quelles situations et selon quels principes, en utilisant divers supports pédagogiques.


Inclut des contenus avancés tels que le calcul des fonctions trigonométriques, l'orthogonalité et la transformée de Fourier.
Après avoir expliqué les bases, les formules importantes et les applications des fonctions trigonométriques, nous abordons des sujets plus avancés tels que le calcul et l'orthogonalité des fonctions trigonométriques, les transformées de Fourier et les développements en astronomie.
L'ensemble de ce contenu repose sur des illustrations détaillées qui vous permettent de constater les principes par vous-même, ainsi que sur des explications claires et concises, fournies par des experts, qui vont droit au but.


Les meilleurs livres scientifiques - Collection Newton Highlights
Newton, un magazine scientifique mensuel, propose à ses lecteurs des articles scientifiques de haute qualité, accompagnés des meilleures photographies et illustrations.
La série « Newton Highlights » est une série scientifique qui publie un volume par mois en réorganisant des articles du magazine « Newton » ayant reçu des critiques particulièrement favorables de la part des lecteurs, sur la base d'un sujet spécifique.
Les quelque 80 volumes apparentés, dont « Tableau périodique », « Théorie de la relativité », « Théorie quantique », « Le corps humain - Anatomie du XXIe siècle » et « Le monde mystérieux des mathématiques », se vendent également bien.