
Voir les mathématiques dans l'histoire coréenne
 |
Description
Introduction au livre
Des temps préhistoriques, il y a des centaines de milliers d'années, à la chute de l'empire coréen en 1910
Nos peuples vivant sur la péninsule coréenne ont toujours été passionnés par les mathématiques ! Depuis les origines mêmes de l'histoire de la péninsule coréenne, divers aspects des mathématiques sont dissimulés dans les institutions, les langues, les jeux, les inventions et les bâtiments créés par nos ancêtres. Quels secrets mathématiques recèle l'histoire coréenne ? Ce livre aborde plus de 20 sujets fascinants de l'histoire coréenne, offrant une explication claire et facile à comprendre de la manière dont nos ancêtres ont utilisé leur sagesse mathématique pour façonner l'histoire. Ce livre offre aux étudiants en sciences humaines un attrait insoupçonné des mathématiques et aux étudiants en sciences, souvent réfractaires à l'histoire, une formation en sciences humaines enrichissante. Il constitue un ouvrage essentiel à notre époque pour inculquer une pensée intégrée et des valeurs aux individus de tous âges. |
- Vous pouvez consulter un aperçu du contenu du livre.
Aperçu
indice
préface
Outils représentatifs de l'ère préhistorique : le nombre d'or et la sphère de révolution _8
La fondation de Gojoseon et le mythe de Dangun : Le nombre 3_20
Les dolmens sont des tombes de l'âge du bronze : Le paradoxe de la roue _34
Yutnori, un jeu très ancien : Nombre de cas et probabilité _44
L'amour du roi Gaero de Baekje pour le go : un affrontement entre les humains et l'intelligence artificielle _54
L'invasion massive de Goguryeo par la dynastie Sui : la signification mathématique d'une armée d'un million d'hommes _64
Musique et instruments anciens : La méthode des profits et pertes en trois parties _76
Objets Silla provenant de l'étang Wolji à Gyeongju : Restauration du Jureunggu à 14 côtés et objets _88
Le Feng Shui dans le mythe fondateur de Goryeo : Yin-Yang, les cinq éléments et diverses formations _100
Le roi Gwangjong de Goryeo a instauré le système d'examens de la fonction publique : questions d'examen de mathématiques de Goryeo _112
Gyerim Yusa, récit de voyage de Goryeo écrit par un envoyé Song : Prononciation et lecture des nombres par les habitants de Goryeo _124
Haeinsa Temple Tripitaka Koreana Woodblocks in Hapcheon: 50 Million Characters and Probability Calculations _134
Palais de Gyeongbokgung, palais royal de Joseon : cycloïdes et tuiles _146
Ha Ryun, conseiller du Taejong : Seunggyeongdo et Origami _160
Le roi Sejong, qui avait lui-même étudié les mathématiques : Études académiques et industrielles de Joseon 172
Le très, très unique Hunminjeongeum : Lettres mathématiques et scientifiques _184
Constitution de Joseon, Gyeongguk Daejeon : Poids et Mesures _198
Peintures d'insectes de l'artiste Shin Saimdang : Insectes et minorités _210
Le grand épéiste de Joseon, Im Kkeok-jeong : La loi de Manghaedo et la mesure des distances _222
Yi Sun-sin et la guerre d'Imjin : la formation en aile de grue et le Dohundo _236
Joseon tel que reflété dans le journal de Hamel : Gusuryak de Choi Seok-jeong _246
Le roi Jeongjo et Jeong Yak-yong, qui ont construit la nouvelle ville de Hwaseong : Grues et poulies _260
Le Daedongyeojido de Kim Jeong-ho, une compilation de la cartographie de Joseon : échelle de 100 Li et échelle _270
« Nouveau livre d’arithmétique » de l’envoyé de La Haye, Lee Sang-seol : un pont entre les mathématiques traditionnelles et modernes _282
Références
Outils représentatifs de l'ère préhistorique : le nombre d'or et la sphère de révolution _8
La fondation de Gojoseon et le mythe de Dangun : Le nombre 3_20
Les dolmens sont des tombes de l'âge du bronze : Le paradoxe de la roue _34
Yutnori, un jeu très ancien : Nombre de cas et probabilité _44
L'amour du roi Gaero de Baekje pour le go : un affrontement entre les humains et l'intelligence artificielle _54
L'invasion massive de Goguryeo par la dynastie Sui : la signification mathématique d'une armée d'un million d'hommes _64
Musique et instruments anciens : La méthode des profits et pertes en trois parties _76
Objets Silla provenant de l'étang Wolji à Gyeongju : Restauration du Jureunggu à 14 côtés et objets _88
Le Feng Shui dans le mythe fondateur de Goryeo : Yin-Yang, les cinq éléments et diverses formations _100
Le roi Gwangjong de Goryeo a instauré le système d'examens de la fonction publique : questions d'examen de mathématiques de Goryeo _112
Gyerim Yusa, récit de voyage de Goryeo écrit par un envoyé Song : Prononciation et lecture des nombres par les habitants de Goryeo _124
Haeinsa Temple Tripitaka Koreana Woodblocks in Hapcheon: 50 Million Characters and Probability Calculations _134
Palais de Gyeongbokgung, palais royal de Joseon : cycloïdes et tuiles _146
Ha Ryun, conseiller du Taejong : Seunggyeongdo et Origami _160
Le roi Sejong, qui avait lui-même étudié les mathématiques : Études académiques et industrielles de Joseon 172
Le très, très unique Hunminjeongeum : Lettres mathématiques et scientifiques _184
Constitution de Joseon, Gyeongguk Daejeon : Poids et Mesures _198
Peintures d'insectes de l'artiste Shin Saimdang : Insectes et minorités _210
Le grand épéiste de Joseon, Im Kkeok-jeong : La loi de Manghaedo et la mesure des distances _222
Yi Sun-sin et la guerre d'Imjin : la formation en aile de grue et le Dohundo _236
Joseon tel que reflété dans le journal de Hamel : Gusuryak de Choi Seok-jeong _246
Le roi Jeongjo et Jeong Yak-yong, qui ont construit la nouvelle ville de Hwaseong : Grues et poulies _260
Le Daedongyeojido de Kim Jeong-ho, une compilation de la cartographie de Joseon : échelle de 100 Li et échelle _270
« Nouveau livre d’arithmétique » de l’envoyé de La Haye, Lee Sang-seol : un pont entre les mathématiques traditionnelles et modernes _282
Références
Image détaillée
Dans le livre
La capacité à fabriquer de la poterie à l'aide d'un tour de potier implique la compréhension du principe de rotation.
En mathématiques, un solide de révolution est une figure tridimensionnelle qui effectue une rotation complète autour d'un axe droit.
Par exemple, une colonne ou un cône que l'on peut observer lorsqu'on fixe une feuille de papier rectangulaire ou triangulaire rectangle sur une baguette en bois et qu'on la fait tourner est un solide de révolution.
---p.
15 outils représentatifs de l'ère préhistorique : le nombre d'or et la sphère de révolution
Pour nos ancêtres, le chiffre 3 était le premier auquel on pouvait associer le mot « tout », et c'était un nombre qui représentait le tout car il incluait le début, le milieu et la fin.
Le pouvoir du chiffre trois est universel et représente la nature tripartite du monde, composé du ciel, de la terre et de la mer.
3 représente le corps humain.
âme .
Elle représente l'esprit, la naissance, la vie et la mort, le début, le milieu et la fin, le passé, le présent et le futur, ainsi que les trois phases de la lune (croissant, demi-lune et pleine lune).
De plus, la base du chiffre 3 est le ciel, la terre et l'homme, et hier (le passé), aujourd'hui (le présent) et demain (le futur).
---p.
31 La fondation de Gojoseon et le mythe de Dangun : parmi les nombres 3
Le Hwangjonggwan, créé par Park Yeon pour obtenir le Hwangjongum, a également influencé le système de poids et mesures.
Dans les sociétés prémodernes, la longueur d'un cheok variait légèrement d'une époque à l'autre et d'une région à l'autre.
Sejong a ressenti le besoin de réorganiser le système de poids et mesures car celui-ci était devenu désorganisé.
Ainsi, sur la base du Hwangjonggwan créé par Park Yeon, le Hwangjongcheok a été établi.
Le Hwangjong-gwan est de 9 chi plus 1 chi pour faire 1 chi (尺, ja), et s'appelle Hwangjong-cheok.
---p.
85 Musique et instruments anciens : d'après la méthode des profits et pertes en trois parties
Un objet rond et brisé, tel que le « Sourire de Silla », peut retrouver sa forme ronde en utilisant le centre du cercle circonscrit d'un triangle.
Pour reconstruire un triangle brisé à l'aide des mathématiques, il faut comprendre comment construire la médiatrice et le centre du cercle circonscrit au triangle.
---p.
97 reliques de Silla provenant de Gyeongju Wolji : une stèle funéraire à 14 côtés et la restauration de reliques
Une caractéristique majeure du mythe fondateur de Goryeo est qu'il sanctifie l'autorité royale à travers la science médiévale du feng shui.
Le Feng Shui considère l'univers, la nature, les différentes structures créées par l'homme et la vie humaine au sein de cet environnement comme un seul organisme.
Les principes vitaux de ces organismes maintiennent un système rigoureusement ordonné, et comme ils sont appliqués de manière répétée et identique dans les mondes macroscopique et microscopique, ce principe s'exprime dans un système numérique complexe, qui constitue l'essence même du Feng Shui.
---p.
103 Le Feng Shui dans le mythe fondateur de Goryeo : Parmi les cinq éléments du yin et du yang et diverses formations
Il y a autre chose de mathématiquement très surprenant dans le Haeinsa Tripitaka Koreana.
Parmi les 52 396 888 caractères du Tripitaka Koreana, il n'y a que 158 fautes de frappe, ce qui est un résultat étonnant, la probabilité de fautes de frappe n'étant que de (%).
Bien que de nombreuses personnes y aient travaillé, il ne comporte quasiment aucune erreur, et le niveau d'écriture et de gravure est étonnant, comme s'il avait été créé par une seule personne.
---p.
141 blocs de bois Haeinsa Tripitaka Koreana réalisés pendant l'invasion mongole : 50 millions de caractères et calculs de probabilité
Sejong n'a pas seulement étudié les mathématiques en résolvant lui-même des problèmes, mais a également encouragé les fonctionnaires, y compris la noblesse, à étudier les sciences et l'ingénierie.
On raconte que lorsque le gouverneur de Gyeongsang-do fit don de 100 volumes du livre de mathématiques « Méthodes mathématiques de Yang Hui » publié dans la Chine des Song, ceux-ci furent répartis équitablement entre le Jiphyeonjeon, le ministère des Impôts et le Seopsan-guk (習算局) du Seoungwan.
C’est ainsi que Sejong prit conscience de l’importance des mathématiques en tant que discipline fondamentale ; il étudia donc lui-même les mathématiques, encouragea les érudits et les chercheurs, et chargea même des érudits de mener des recherches et des enquêtes.
---p.
176 Le roi Sejong, qui étudia lui-même les mathématiques : le monde industriel et académique de Joseon
《Gusuryak》 contient l'origine et les fondements des nombres, les méthodes de représentation des fractions et leurs calculs, la somme des séries additionnées à l'aide de règles et les équations simultanées.
De plus, la forme des branches de la montagne et la méthode d'agencement de ces branches pour l'addition, la soustraction et la multiplication sont expliquées dans la section « Nombres ».
---p.
252 Joseon tel que reflété dans le journal de Hamel : Extrait du Gusuryak de Choi Seok-jeong
Kim Jeong-ho a conçu un certain nombre de symboles pour faciliter la reconnaissance rapide et facile des nombreux noms de lieux, au nombre d'environ 11 700, et a organisé ces symboles dans une sorte de légende appelée « carte » pour aider les utilisateurs à comprendre.
En mathématiques, un solide de révolution est une figure tridimensionnelle qui effectue une rotation complète autour d'un axe droit.
Par exemple, une colonne ou un cône que l'on peut observer lorsqu'on fixe une feuille de papier rectangulaire ou triangulaire rectangle sur une baguette en bois et qu'on la fait tourner est un solide de révolution.
---p.
15 outils représentatifs de l'ère préhistorique : le nombre d'or et la sphère de révolution
Pour nos ancêtres, le chiffre 3 était le premier auquel on pouvait associer le mot « tout », et c'était un nombre qui représentait le tout car il incluait le début, le milieu et la fin.
Le pouvoir du chiffre trois est universel et représente la nature tripartite du monde, composé du ciel, de la terre et de la mer.
3 représente le corps humain.
âme .
Elle représente l'esprit, la naissance, la vie et la mort, le début, le milieu et la fin, le passé, le présent et le futur, ainsi que les trois phases de la lune (croissant, demi-lune et pleine lune).
De plus, la base du chiffre 3 est le ciel, la terre et l'homme, et hier (le passé), aujourd'hui (le présent) et demain (le futur).
---p.
31 La fondation de Gojoseon et le mythe de Dangun : parmi les nombres 3
Le Hwangjonggwan, créé par Park Yeon pour obtenir le Hwangjongum, a également influencé le système de poids et mesures.
Dans les sociétés prémodernes, la longueur d'un cheok variait légèrement d'une époque à l'autre et d'une région à l'autre.
Sejong a ressenti le besoin de réorganiser le système de poids et mesures car celui-ci était devenu désorganisé.
Ainsi, sur la base du Hwangjonggwan créé par Park Yeon, le Hwangjongcheok a été établi.
Le Hwangjong-gwan est de 9 chi plus 1 chi pour faire 1 chi (尺, ja), et s'appelle Hwangjong-cheok.
---p.
85 Musique et instruments anciens : d'après la méthode des profits et pertes en trois parties
Un objet rond et brisé, tel que le « Sourire de Silla », peut retrouver sa forme ronde en utilisant le centre du cercle circonscrit d'un triangle.
Pour reconstruire un triangle brisé à l'aide des mathématiques, il faut comprendre comment construire la médiatrice et le centre du cercle circonscrit au triangle.
---p.
97 reliques de Silla provenant de Gyeongju Wolji : une stèle funéraire à 14 côtés et la restauration de reliques
Une caractéristique majeure du mythe fondateur de Goryeo est qu'il sanctifie l'autorité royale à travers la science médiévale du feng shui.
Le Feng Shui considère l'univers, la nature, les différentes structures créées par l'homme et la vie humaine au sein de cet environnement comme un seul organisme.
Les principes vitaux de ces organismes maintiennent un système rigoureusement ordonné, et comme ils sont appliqués de manière répétée et identique dans les mondes macroscopique et microscopique, ce principe s'exprime dans un système numérique complexe, qui constitue l'essence même du Feng Shui.
---p.
103 Le Feng Shui dans le mythe fondateur de Goryeo : Parmi les cinq éléments du yin et du yang et diverses formations
Il y a autre chose de mathématiquement très surprenant dans le Haeinsa Tripitaka Koreana.
Parmi les 52 396 888 caractères du Tripitaka Koreana, il n'y a que 158 fautes de frappe, ce qui est un résultat étonnant, la probabilité de fautes de frappe n'étant que de (%).
Bien que de nombreuses personnes y aient travaillé, il ne comporte quasiment aucune erreur, et le niveau d'écriture et de gravure est étonnant, comme s'il avait été créé par une seule personne.
---p.
141 blocs de bois Haeinsa Tripitaka Koreana réalisés pendant l'invasion mongole : 50 millions de caractères et calculs de probabilité
Sejong n'a pas seulement étudié les mathématiques en résolvant lui-même des problèmes, mais a également encouragé les fonctionnaires, y compris la noblesse, à étudier les sciences et l'ingénierie.
On raconte que lorsque le gouverneur de Gyeongsang-do fit don de 100 volumes du livre de mathématiques « Méthodes mathématiques de Yang Hui » publié dans la Chine des Song, ceux-ci furent répartis équitablement entre le Jiphyeonjeon, le ministère des Impôts et le Seopsan-guk (習算局) du Seoungwan.
C’est ainsi que Sejong prit conscience de l’importance des mathématiques en tant que discipline fondamentale ; il étudia donc lui-même les mathématiques, encouragea les érudits et les chercheurs, et chargea même des érudits de mener des recherches et des enquêtes.
---p.
176 Le roi Sejong, qui étudia lui-même les mathématiques : le monde industriel et académique de Joseon
《Gusuryak》 contient l'origine et les fondements des nombres, les méthodes de représentation des fractions et leurs calculs, la somme des séries additionnées à l'aide de règles et les équations simultanées.
De plus, la forme des branches de la montagne et la méthode d'agencement de ces branches pour l'addition, la soustraction et la multiplication sont expliquées dans la section « Nombres ».
---p.
252 Joseon tel que reflété dans le journal de Hamel : Extrait du Gusuryak de Choi Seok-jeong
Kim Jeong-ho a conçu un certain nombre de symboles pour faciliter la reconnaissance rapide et facile des nombreux noms de lieux, au nombre d'environ 11 700, et a organisé ces symboles dans une sorte de légende appelée « carte » pour aider les utilisateurs à comprendre.
---p.
278 Le Daedongyeojido de Kim Jeong-ho, une compilation de cartographie de Joseon : à partir de l’échelle de 100 ri et de l’échelle
278 Le Daedongyeojido de Kim Jeong-ho, une compilation de cartographie de Joseon : à partir de l’échelle de 100 ri et de l’échelle
Avis de l'éditeur
Une rencontre de haut niveau entre les sciences humaines et les sciences naturelles !
Le professeur Lee Gwang-yeon, l'auteur, explique les mathématiques de manière simple et ludique à travers différents ouvrages.
C'est un auteur qui réfléchit constamment à la manière de rendre les mathématiques plus accessibles au grand public.
Dans son précédent ouvrage, « Quand les mathématiques rencontrent l'histoire mondiale », il avait sélectionné vingt-huit scènes passionnantes de l'histoire mondiale et expliqué de manière intéressante comment les mathématiques avaient entraîné des changements dans ces scènes.
Cette fois-ci, nous présentons des théories mathématiques passionnantes qui s'appliquent à 24 thèmes de l'histoire coréenne, incluant des personnes, des événements et des vestiges.
En tant que mathématicien, il peut être naturel d'expliquer les mathématiques de manière simple et ludique, mais les intérêts variés de l'auteur, notamment sa connaissance de l'histoire mondiale et de l'histoire coréenne, sont également intéressants.
Pour ceux qui s'intéressent à la fois aux mathématiques et à l'histoire, cela pourrait être une occasion amusante d'étudier les mathématiques à travers le prisme d'autres disciplines.
Lorsque vous lisez avec intérêt des récits de l'histoire coréenne, les mathématiques vous viennent naturellement.
Le roi Gaero de Baekje a perdu la vie parce qu'il aimait tellement le baduk.
Sous la dynastie Joseon, le roi Sejong étudia les mathématiques avec plus d'assiduité que quiconque.
Shin Saimdang a peint et brodé toutes sortes d'herbes et d'insectes sur un paravent pliant à huit panneaux.
Lee Sang-seol, dépêché comme envoyé spécial à La Haye, a lui-même créé un livre de mathématiques.
En suivant les histoires du roi Sejong, de dame Shin Saimdang et de Lee Sang-seol, nous découvrons que des mathématiques intéressantes sont imbriquées dans leur vie.
De plus, les mathématiciens ayant vécu sous les dynasties Goryeo et Joseon importaient des ouvrages de mathématiques chinois, les mémorisaient et les utilisaient dans leurs systèmes et leur vie quotidienne.
Si vous écoutez les histoires des livres de mathématiques et des méthodes d'étude qu'ils ont utilisées, les mathématiques que nous étudions aujourd'hui ne vous paraîtront peut-être pas si difficiles.
Découvrir les secrets mathématiques cachés dans notre histoire, souvent négligés.
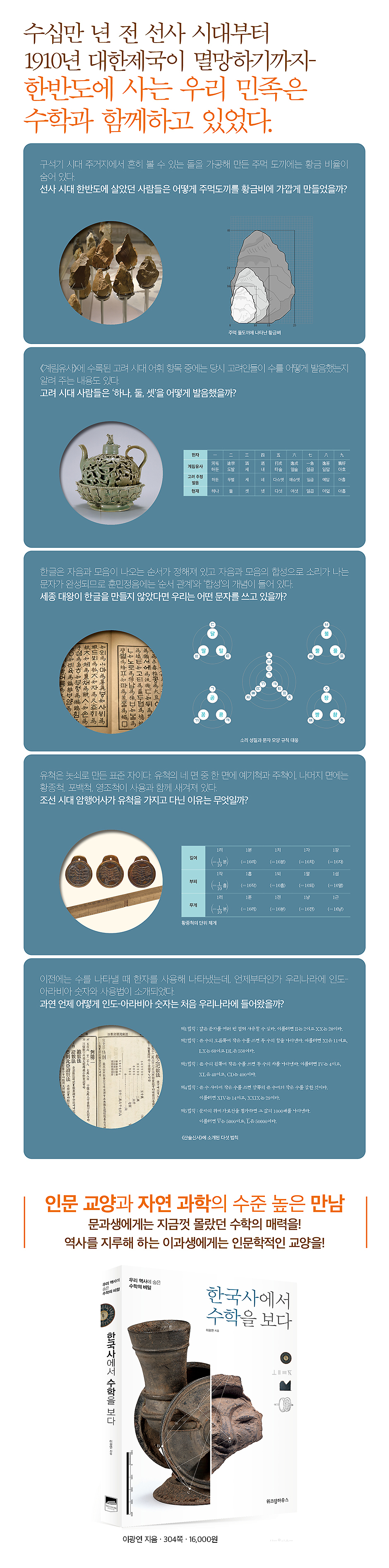
Comment les habitants de la dynastie Goryeo prononçaient-ils « un, deux, trois » ? Si le roi Sejong le Grand n’avait pas créé le hangeul, quel alphabet utiliserions-nous aujourd’hui ? Et quand les chiffres indo-arabes ont-ils été introduits en Corée ? Ce livre offre un éclairage sur les mathématiques liées à l’histoire coréenne, souvent méconnu.
Grâce à la lecture des nombres par le peuple Goryeo dans le « Gyerim Yusa » et le « Hunminjeongeum Eonhae », nous pouvons voir quels principes mathématiques et scientifiques ont été utilisés pour créer le Hangul.
Il présente également les contenus relatifs aux chiffres indo-arabes qui apparaissent dans le « Nouveau livre d'arithmétique ».
De plus, il est riche en documents photographiques et en images mathématiques variés pour aider les lecteurs à comprendre facilement l'histoire et les mathématiques, ce qui rend sa lecture visuellement agréable.
Le professeur Lee Gwang-yeon, l'auteur, explique les mathématiques de manière simple et ludique à travers différents ouvrages.
C'est un auteur qui réfléchit constamment à la manière de rendre les mathématiques plus accessibles au grand public.
Dans son précédent ouvrage, « Quand les mathématiques rencontrent l'histoire mondiale », il avait sélectionné vingt-huit scènes passionnantes de l'histoire mondiale et expliqué de manière intéressante comment les mathématiques avaient entraîné des changements dans ces scènes.
Cette fois-ci, nous présentons des théories mathématiques passionnantes qui s'appliquent à 24 thèmes de l'histoire coréenne, incluant des personnes, des événements et des vestiges.
En tant que mathématicien, il peut être naturel d'expliquer les mathématiques de manière simple et ludique, mais les intérêts variés de l'auteur, notamment sa connaissance de l'histoire mondiale et de l'histoire coréenne, sont également intéressants.
Pour ceux qui s'intéressent à la fois aux mathématiques et à l'histoire, cela pourrait être une occasion amusante d'étudier les mathématiques à travers le prisme d'autres disciplines.
Lorsque vous lisez avec intérêt des récits de l'histoire coréenne, les mathématiques vous viennent naturellement.
Le roi Gaero de Baekje a perdu la vie parce qu'il aimait tellement le baduk.
Sous la dynastie Joseon, le roi Sejong étudia les mathématiques avec plus d'assiduité que quiconque.
Shin Saimdang a peint et brodé toutes sortes d'herbes et d'insectes sur un paravent pliant à huit panneaux.
Lee Sang-seol, dépêché comme envoyé spécial à La Haye, a lui-même créé un livre de mathématiques.
En suivant les histoires du roi Sejong, de dame Shin Saimdang et de Lee Sang-seol, nous découvrons que des mathématiques intéressantes sont imbriquées dans leur vie.
De plus, les mathématiciens ayant vécu sous les dynasties Goryeo et Joseon importaient des ouvrages de mathématiques chinois, les mémorisaient et les utilisaient dans leurs systèmes et leur vie quotidienne.
Si vous écoutez les histoires des livres de mathématiques et des méthodes d'étude qu'ils ont utilisées, les mathématiques que nous étudions aujourd'hui ne vous paraîtront peut-être pas si difficiles.
Découvrir les secrets mathématiques cachés dans notre histoire, souvent négligés.
Comment les habitants de la dynastie Goryeo prononçaient-ils « un, deux, trois » ? Si le roi Sejong le Grand n’avait pas créé le hangeul, quel alphabet utiliserions-nous aujourd’hui ? Et quand les chiffres indo-arabes ont-ils été introduits en Corée ? Ce livre offre un éclairage sur les mathématiques liées à l’histoire coréenne, souvent méconnu.
Grâce à la lecture des nombres par le peuple Goryeo dans le « Gyerim Yusa » et le « Hunminjeongeum Eonhae », nous pouvons voir quels principes mathématiques et scientifiques ont été utilisés pour créer le Hangul.
Il présente également les contenus relatifs aux chiffres indo-arabes qui apparaissent dans le « Nouveau livre d'arithmétique ».
De plus, il est riche en documents photographiques et en images mathématiques variés pour aider les lecteurs à comprendre facilement l'histoire et les mathématiques, ce qui rend sa lecture visuellement agréable.
SPÉCIFICATIONS DES PRODUITS
- Date de publication : 18 juin 2020
Nombre de pages, poids, dimensions : 304 pages | 502 g | 152 × 215 × 30 mm
- ISBN13 : 9791190786782
- ISBN10 : 1190786788
Vous aimerez peut-être aussi
카테고리
Langue coréenne


Langue coréenne


![ELLE 엘르 스페셜 에디션 A형 : 12월 [2025]](http://librairie.coreenne.fr/cdn/shop/files/b8e27a3de6c9538896439686c6b0e8fb.jpg?v=1766436872&width=3840)























